Trees | CSE205 : DATA STRUCTURES AND ALGORITHMS | B.Tech CSE

Trees

A tree is a non-linear hierarchical data structure that consists of nodes connected by edges.

⭐Tree Terminologies:

1) Node:

• A node is an entity that contains a key or value and pointers to its child nodes.
• The last nodes of each path are called leaf nodes or external nodes that do not contain a link/pointer to child nodes.
• The node having at least a child node is called an internal node.

2) Edge:

• It is the link between any two nodes.

3) Root:

• It is the topmost node of a tree.

4) Height of a Node:

• The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).

5)Depth of a Node:

• The depth of a node is the number of edges from the root to the node.

6)Height of a Tree:

• The height of a Tree is the height of the root node or the depth of the deepest node.

7) Degree of a Node:

• The degree of a node is the total number of branches of that node.

8) Forest:

• A collection of disjoint trees is called a forest.

⭐Tree Types:

1) Binary Tree

• Each node has up to two children: a left child and a right child.
• No specific ordering of nodes.

2) Binary Search Tree (BST)

• A binary tree with the property: left child < parent < right child.
• Useful for fast searching, insertion, and deletion operations.

3) AVL Tree (Adelson-Velsky and Landis Tree)

• A self-balancing binary search tree.
• Balances itself by ensuring the heights of the left and right subtrees differ by no more than one.
• Provides better time complexity for search, insertion, and deletion.

4) Heap (Binary Heap)

• A complete binary tree where every parent node has a specific order relationship with its children.
• Min-Heap: Parent nodes have values less than or equal to children.
• Max-Heap: Parent nodes have values greater than or equal to children.
• Used in priority queues and heapsort.

5) B-Tree

• A self-balancing tree designed for systems that read and write large blocks of data, such as databases.
• Nodes can have multiple children.
• B-Trees are a generalization of binary search trees with higher "order," which allows more data per node.

6) B+ Tree

• An extension of B-Tree where all values are stored in leaf nodes.
• Leaf nodes are linked, providing sequential access.
• Commonly used in database indexing and file systems.

⭐Binary Tree:

• A binary tree is a tree data structure in which each parent node can have at most two children.

• Root: The topmost node in the tree
• Parent: A node with a child or children
• Child: A node extended from another node (parent node)
• Leaf: A node without a child

⭐Types of Binary Tree:

1) Full Binary Tree:

• A full binary tree is a special type of binary tree in which every parent node/internal node has either two or no children.

2) Perfect Binary Tree:

• A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.

3) Complete Binary Tree:

• A complete binary tree is just like a full binary tree, but with two major differences,
• Every level must be completely filled
• All the leaf elements must lean towards the left.
• The last leaf element might not have a right sibling i.e. a complete binary tree doesn't have to be a full binary tree.

4) Degenerate or Pathological Tree:

• A degenerate or pathological tree is the tree having a single child either left or right.

5) Skewed Binary Tree:

• A skewed binary tree is a pathological/degenerate tree in which the tree is either  dominated by the left nodes or the right nodes.
• There are two types of skewed binary tree: 
• left-skewed binary tree
• right-skewed binary tree

6) Balanced Binary Tree:

• It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1.

⭐Binary Tree Representation:

CODE:

struct node{
    int data;
    struct node *left;
    struct node *right;
};

⭐Binary Tree - Array Representation:

• Assigning of indexes is done in this way :
• Index of parent = INT [index of child node / 2] 
• Index of Left Child = 2 * Index of parent 
• Index of Right Child = 2 * Index of parent + 1

⭐Binary Tree - Linked List Representation:

• In a double linked list, every node consists of three fields. 
• First field for storing left child address, 
• Second for storing actual data and 
• Third for storing right child address.

⭐Operations of Binary Tree Data Structure:

• Create: Creates a tree in the data structure
• Insert: Inserts data in a tree
• Search: Searches specific data in a tree to check if it is present or not
• Traversal:
• Pre-order Traversal: perform Traveling a tree in a pre-order manner
• In-order Traversal: perform Traveling a tree in an in-order manner
• Post-order Traversal: perform Traveling a tree in a post-order manner

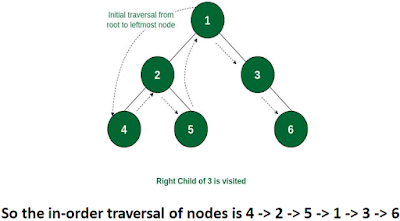
⭐Binary Trees: In-order Traversal:

• follows the Left-Root-Right pattern
• In-order traversal: Traverse left subtree → Visit root → Traverse right subtree

CODE:

#include <iostream>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// Function for in-order traversal using recursion
void inorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    inorderTraversal(root->left);
    cout << root->val << " ";
    inorderTraversal(root->right);
}

int main() {
    // Create a simple binary tree
    //       1
    //      / \
    //     2   3
    //    / \
    //   4   5

    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    cout << "Inorder Traversal: ";
    inorderTraversal(root);
    cout << endl;

    return 0;
}

OUTPUT:

Inorder Traversal: 4 2 5 1 3

⭐Binary Trees: Pre-order Traversal:

• follows the Root-Left-Right pattern
• Pre-order traversal: Visit root → Traverse left subtree → Traverse right subtree

CODE:

#include <iostream>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// Function for preorder traversal using recursion
void preorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    cout << root->val << " ";
    preorderTraversal(root->left);
    preorderTraversal(root->right);
}

int main() {
    // Create a simple binary tree
    //       1
    //      / \
    //     2   3
    //    / \
    //   4   5

    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    cout << "Preorder Traversal: ";
    preorderTraversal(root);
    cout << endl;

    return 0;
}

OUTPUT:

Preorder Traversal: 1 2 4 5 3 

⭐Binary Trees: Post-order Traversal:

• follows the Left-Right-Root pattern
• Post-order traversal: Traverse left subtree → Traverse right subtree → Visit root

CODE:

#include <iostream>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// Function for postorder traversal using recursion
void postorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    postorderTraversal(root->left); 
    postorderTraversal(root->right);  
    cout << root->val << " ";             
}

int main() {
    // Create a simple binary tree
    //       1
    //      / \
    //     2   3
    //    / \
    //   4   5

    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    cout << "Postorder Traversal: ";
    postorderTraversal(root);
    cout << endl;

    return 0;
}

OUTPUT:

Postorder Traversal: 4 5 2 3 1 

⭐Binary Search Tree:

• A Binary Search Tree (BST) is a type of binary tree in which the data is organized and stored in a sorted order.
• every value on the left subtree < parent node < right subtree value.

CODE:

#include <iostream>
using namespace std;

// Node structure for a Binary Search Tree
struct Node {
    int data;
    Node* left;
    Node* right;
};

// Function to create a new Node
Node* createNode(int data){
    Node* newNode = new Node();
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to insert a node in the BST
Node* insertNode(Node* root, int data){
    if (root == nullptr) {
        return createNode(data);
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    }
    else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }

    return root;
}

// Function to do inorder traversal of BST
void inorderTraversal(Node* root){
    if (root != nullptr) {
        inorderTraversal(root->left);
        cout << root->data << " ";
        inorderTraversal(root->right);
    }
}

// Function to search a given key in a given BST
Node* searchNode(Node* root, int key){
    if (root == nullptr || root->data == key) {
        return root;
    }

    if (root->data < key) {
        return searchNode(root->right, key);
    }

    return searchNode(root->left, key);
}

// Function to find the inorder successor
Node* minValueNode(Node* node){
    Node* current = node;
    while (current && current->left != nullptr) {
        current = current->left;
    }
    return current;
}

// Function to delete a node
Node* deleteNode(Node* root, int data){
    if (root == nullptr)
        return root;

    if (data < root->data) {
        root->left = deleteNode(root->left, data);
    }
    else if (data > root->data) {
        root->right = deleteNode(root->right, data);
    }
    else {
        if (root->left == nullptr) {
            Node* temp = root->right;
            delete root;
            return temp;
        }
        else if (root->right == nullptr) {
            Node* temp = root->left;
            delete root;
            return temp;
        }

        Node* temp = minValueNode(root->right);
        root->data = temp->data;
        root->right = deleteNode(root->right, temp->data);
    }

    return root;
}

int main(){

    Node* root = nullptr;

    // create a BST
    root = insertNode(root, 50);
    root = insertNode(root, 30);
    root = insertNode(root, 20);
    root = insertNode(root, 40);
    root = insertNode(root, 70);
    root = insertNode(root, 60);
    root = insertNode(root, 80);

    // Print the inorder traversal of a BST
    cout << "Inorder traversal of the given Binary Search "
            "Tree is: ";
    inorderTraversal(root);
    cout << endl;

    // delete a node in BST
    root = deleteNode(root, 20);
    cout << "After deletion of 20: ";
    inorderTraversal(root);
    cout << endl;

    // Insert a node in BST
    root = insertNode(root, 25);
    cout << "After insertion of 25: ";
    inorderTraversal(root);
    cout << endl;

    // Search a key in BST
    Node* found = searchNode(root, 25);

    // check if the key is found or not
    if (found != nullptr) {
        cout << "Node 25 found in the BST." << endl;
    }
    else {
        cout << "Node 25 not found in the BST." << endl;
    }

    return 0;
}

OUTPUT:

Inorder traversal of the given Binary Search Tree is: 20 30 40 50 60 70 80 

After deletion of 20: 30 40 50 60 70 80 

After insertion of 25: 25 30 40 50 60 70 80 

Node 25 found in the BST.

---

🚨Thanks for visiting classpdfindia✨

Welcome to a hub for 😇Nerds and knowledge seekers! Here, you'll find everything you need to stay updated on education, notes, books, and daily trends.

💗 Bookmark our site to stay connected and never miss an update!

💌 Have suggestions or need more content? Drop a comment below, and let us know what topics you'd like to see next! Your support means the world to us. 😍